Reiknirit, reiknihugsun og forritun: Nýjar áherslur í námskrá

Bjarnheiður Kristinsdóttir, Freyja Hreinsdóttir, Ingólfur Gíslason og Jóhann Örn Sigurjónsson.

Nútímasamfélag er undirlagt reikniritum (e. algorithms). Reiknirit er nákvæmlega skilgreind röð af aðgerðum sem skila tiltekinni niðurstöðu út frá gefnum forsendum. Oftast eru reiknirit gerð til að leysa ákveðið verkefni. Hugsið til dæmis um hvernig þið leggið saman tölurnar 13 og 18 (eða einhverjar aðrar tveggja stafa tölur) og prófið að lýsa því hvernig þið farið að. Ef lýsingin er þannig úr garði gerð að aðrir geti fylgt henni þá er um reiknirit að ræða.

Reiknirit liggja að baki ýmsu í samfélaginu. Meðal annars reikna þau út:

• hvaða fólk kemst á þing eftir að atkvæði í kosningum hafa verið talin,
• hvaða auglýsing birtist næst í vafranum,
• mánaðarlegar afborganir af lánum,
• hvernig spjallmenni svarar spurningu,
• hvar næsta kaffihús er á kortinu í símanum,
• hvernig snjallúr virkar,
• hvert flugvél skuli stefna,
• hvernig ryksuguvélmenni ferðast um íbúð.

Reiknirit hafa þannig talsverð áhrif á daglegan veruleika okkar þrátt fyrir að við skynjum ekki endilega þau ótal reiknirit sem eru að verki og stýra svo mörgu. Við vitum ekki hvað þau eru nákvæmlega að reikna. Þau eru skrifuð af fólki og eru yfirleitt framkvæmd (keyrð) í tölvum, vélum og tækjum, þar sem þau eru útfærð sem forrit (e. program). Forrit er framsetning á reikniriti sem hentar tölvu, það er að segja röð leiðbeininga sem tölva fylgir til að vinna visst verkefni. Dæmi um forrit sem mörg kannast við eru ritvinnsluforrit og tölvuleikir.

Í nýlega uppfærðum stærðfræðihluta aðalnámskrár (2024) eru í fyrsta skipti hæfniviðmið tengd reiknihugsun og forritun en einnig kemur fram að nemendur skuli öðlast hæfni í því að nota upplýsingatækni í stærðfræði og í stuðningsefni er vísað í notkun kvikra rúmfræðiforrita á borð við GeoGebru. Þó að reiknihugsun og forritun séu ný hugtök í stærðfræðihluta aðalnámskrár á Íslandi hafa þau lengi verið hluti af námskrám á Norðurlöndum auk margra annarra landa í Evrópu (Bocconi og félagar, 2022). Einnig er reiknihugsun nú í stærðfræðiramma PISA rannsóknarinnar (OECD, 2022) enda hefur vægi forritunar í rannsóknum og þróun, bæði í háskólum og fyrirtækjum aukist mikið á síðustu árum. Reiknihugsun og forritun í stærðfræðihluta aðalnámskrár miða þó ekki að því að kenna nemendum tiltekin forritunarmál (e. programming language) eða gera nemendur að atvinnuforriturum. Markmiðið er að nemendur skilji, geti gagnrýnt og haft áhrif á þau reiknirit sem eru víða að verki í samfélagi okkar.

Reiknirit hafa verið til í árþúsundir og byggja á gömlum grunni frá því löngu áður en hægt var að láta tölvur framkvæma þau. Eftir að vinnu við útreikninga var útvistað til véla hafa afl og notkunarmöguleikar reiknirita margfaldast. Eitt af því sem er mikilvægt fyrir nútímamanneskju að skilja er hvað hægt sé að láta tölvur gera og hvað ekki.

Þetta er á vissan hátt spurning um það hvað hægt sé að reikna út og hvað ekki. Skilningur á þessu er falinn í reiknihugsun (e. computational thinking).

Nánar um reiknihugsun

Reiknihugsun er vitsmunaferli sem felur það í sér að setja fram verkefni og lausnaraðferð þess á þann hátt að tölva (eða hver sem reiknar) geti fylgt aðferðinni og leyst verkefnið. Slík aðferð fellur undir það sem kallast reiknirit. Reiknihugsun hefur líka verið nefnd hugsunarháttur forritunar og tölvunarhugsun. Reiknihugsun má rekja aftur til verka Seymour Papert (1980) en Jeanette Wing kom hugtakinu á kortið með stuttri grein árið 2006. Hún skilgreindi reiknihugsun sem það að „leysa vandamál, hanna kerfi, og skilja mannlega hegðun, með því að byggja á grundvallarhugtökum tölvunarfræðinnar“ (Wing, 2006, bls. 33). Ekki er allt fræðafólk sammála um nákvæma merkingu hugtaksins reiknihugsun en þó er samkomulag um eftirfarandi meginþætti:

• að brjóta verkefni niður í smærri einingar (e. decomposition) sem svo eru leystar hverjar fyrir sig;
• að koma auga á mynstur (e. pattern recognition) í gögnum eða aðferðum og taka þannig eftir endurteknum eða svipuðum ferlum í verkefnum;
• að hanna og nota abstraksjónir (e. abstraction) eða með öðrum orðum að draga fram mikilvæga eiginleika fyrirbæra en leyfa sér að gleyma eða líta fram hjá smærri atriðum;
• að hugsa og setja fram lausn sem röð af nákvæmlega skilgreindum skrefum sem hver sem er, tölva eða manneskja, getur farið eftir – sumsé að búa til reiknirit (e. algorithm) til að leysa verkefni.

Dæmi 1: Að teikna ferning

Í nýjum hæfniviðmiðum fyrir reiknihugsun og forritun við lok 4. bekkjar kemur fram að nemandi geti „búið til einföld reiknirit og tjáð þau með því að nota breytur, skilyrði og lykkjur“. Þetta er metnaðarfullt og þess virði að útskýra við hvað er átt.

Breyta eða breytistærð (e. variable) í forritun er frábrugðin breytu í stærðfræði. Lýsa má breytu í forritun sem nafngreindu íláti eða hólfi sem geymir upplýsingar sem tölvan notar og getur breytt.

Skilyrði (e. conditional) í forritun segir tölvunni hvað á að gera ef eitthvað er satt og hvað á að gera ef það er ósatt.

Lykkja (e. loop) er röð af aðgerðum sem eru endurteknar.

Skoðum dæmi um reiknirit sem gjarnan er unnið með nemendum á yngsta stigi. Hvernig er hægt að teikna ferning, svo sem í snjó eða sand? Hér er skref-fyrir-skref lýsing:

1. Farðu áfram 10 skref
2. Snúðu þér 90° til hægri
3. Farðu áfram 10 skref
4. Snúðu þér 90° til hægri
5. Farðu áfram 10 skref
6. Snúðu þér 90° til hægri
7. Farðu áfram 10 skref
8. Snúðu þér 90° til hægri

Þessa lýsingu mætti þróa áfram og útfæra með lykkju:

Endurtaktu fjórum sinnum:

1. Farðu áfram 10 skref
2. Snúðu þér 90° til hægri

Þannig verða leiðbeiningarnar styttri og auðlæsilegri.

Einnig má útfæra lykkjuna með skilyrði og breytu:

Í upphafi er n = 0

Á meðan n < 4 skaltu endurtaka:

1. Farðu áfram 10 skref
2. Snúðu þér 90° til hægri
3. Hækkaðu n um 1

Í þessari lykkju var breytan n skilgreind og skipanaröðin endurtekin að gefnu því skilyrði að n sé lægri tala en 4. Lykkjur eru mjög oft þannig að skipanirnar sem í henni felast eru endurteknar með einhverjum reglulegum tilbrigðum að því gefnu að eitthvert skilyrði sé uppfyllt.

Dæmi 2: Að teikna reglulegan marghyrning

Hér er annað verkefni: Hvernig er hægt láta tölvu teikna reglulegan marghyrning með hvaða fjölda hliða sem er? Sama reikniritið á að geta skilað jafnhliða þríhyrningi, ferningi, reglulegum fimmhyrningi og n-hyrningi fyrir hvaða heiltölu n > 2 sem er. Við sem hönnum reikniritið þurfum að hafa í huga hvers konar fyrirmæli tölvan skilur. Byrjum á að hugsa okkur hvernig við gætum sagt manneskju með penna hvernig hún ber sig að. Við gerum ráð fyrir að hún geti gert tvennt: 1) teiknað beint strik af gefinni lengd og 2) snúið stefnunni sem hún teiknar strikið hverju sinni.

Oft er gott að hugsa um eitt tiltekið dæmi fyrst um sinn. Í dæmi 1 sáum við reiknirit til að teikna ferning. Reikniritið sem lýsti teikningu fernings mætti til dæmis útfæra í sjónræna forritunarumhverfinu Scratch. Þar sem 10 skref á tölvuskjá eru afar stutt vegalengd þá breytum við úr 10 skrefum í 100 skref og skrifum forritið á eftirfarandi hátt:

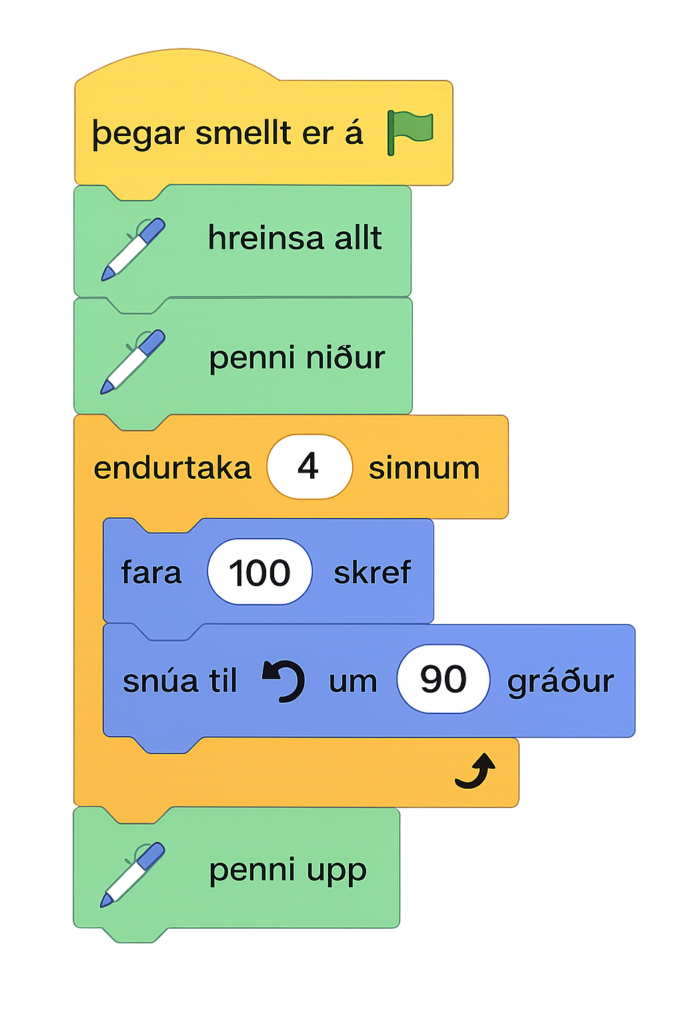
Fyrstu þrjár blokkirnar eru skipanir sem bætt er við af tæknilegum ástæðum. Setja þarf forritið í gang með því að smella á grænt flagg, segja þarf hvaða verkfæri er notað (hér er það penni) og skjáinn þarf að hreinsa í upphafi.

Útkoman þegar við keyrum forritið verður þessi:

Svona er hægt að teikna ferning. En hvað með reglulegan þríhyrning, fimmhyrning, sexhyrning og svo framvegis? Við tökum eftir því að það ætti að vera hægt að teikna aðra reglulega marghyrninga með svipuðum hætti, það er með því að endurtaka hæfilega oft það að teikna strik og snúa hæfilega mikið. Hér höfum við komið auga á mynstur: eitthvað sem er eins við marga ólíka hluti, einhver regluleiki. Við höfum líka dregið út þann eiginleika sem skiptir máli, sem er fjöldi horna. Við getum líka sagt í leiðinni að við höfum brotið verkefnið niður í minni verkefni, frá því að teikna heilan ferning í það að teikna strik og snúa fjórum sinnum.

Nú þurfum við að leysa stærðfræðiverkefnið og spyrjum okkur: Um hve margar gráður þarf að snúa teiknistefnunni þegar við teiknum reglulegan n-hyrning? Sú rannsókn ætti að leiða í ljós að við getum reiknað stærð snúningsins með stæðunni 360°/n. Nú notum við okkur breytistærð (e. variable) til þess að halda utan um fjölda horna og hæfilegan snúning.

Reiknirit:

Setjum n = fjöldi horna

Reiknum gráðutölu hvers horns og köllum hana g, það er g = 360°/n.

Setjum pennann niður

Endurtökum eftirfarandi aðgerðaröð n sinnum:

Förum áfram 100 skref

Snúum teiknistefnunni um g

Í forritunarmálinu Scratch getur samsvarandi forrit litið svona út ef við veljum bókstafinn g til að tákna gráðutölu snúningsins:

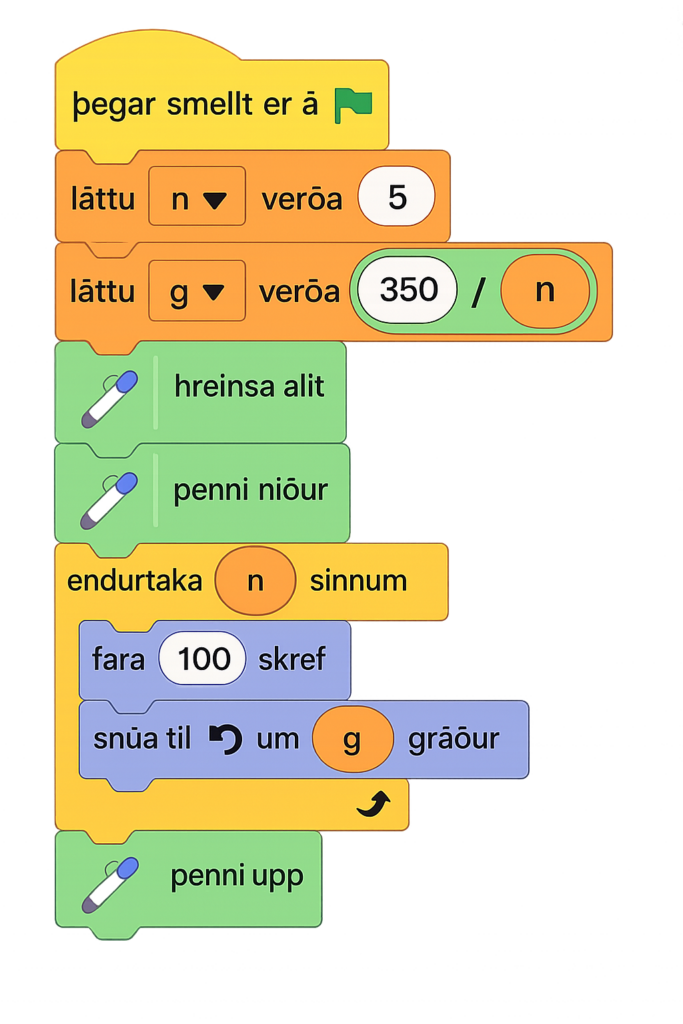
Útkoman þegar n = 5 væri þá þessi:

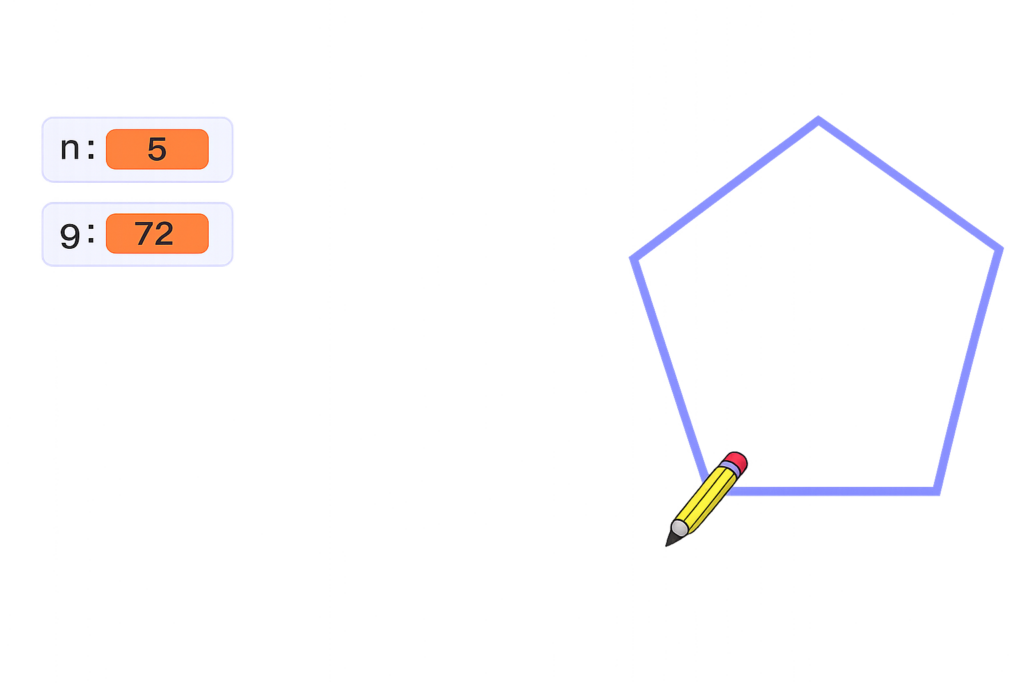
Ef við keyrum þetta forrit til þess að teikna reglulegan 20-hyrning lendum við í vanda: Myndin verður of stór þegar strikin eru af sömu lengd og áður (100 skref). Því þarf að þróa forritið áfram og finna leið til þess að minnka skrefafjöldann eftir því sem fjöldi hliða eykst. Það getur verið verkefni fyrir lesandann að velta fyrir sér hvernig megi útfæra þetta (til dæmis með því að kynna nýja breytu fyrir skrefafjöldann og nýta skilyrði).

Í þessu dæmi sáum við hvernig leysa mátti verkefni með reiknihugsun, það er að segja með því að koma auga á mynstur, hanna og nota abstraksjónir, brjóta verkefni og mynstur niður í minni einingar, búa til reiknirit og að lokum tölvuforrit til að leysa verkefnið. Við notuðum tvær breytur (n og g) og eina lykkju (endurtaka n sinnum) í forritinu.

Forrit

Forrit tekur yfirleitt inntak, til dæmis tvær tölur, og reiknar út frá því þannig að til verði úttak, til dæmis summa tveggja talna. Forritið hér að ofan tekur inn fjölda hliða og „reiknar út“ marghyrning (í formi myndar á skjá). Með því að setja saman forrit getum við meðal annars

• búið til hreyfimynd,
• sett fram líkön af kvikum aðstæðum og
• nýtt gagnvirkni.

Dæmi um þetta væru hreyfimynd af fiski að synda, líkan af hraunflæði frá eldgosi og hnappur í tölvuleik sem lætur kengúru hoppa þegar smellt er á hann. Ýmis grundvallarhugtök í stærðfræði koma við sögu til að gera þetta mögulegt. Meðal þeirra eru breytistærðir, jöfnur, ójöfnur, hnit og föll. Auk þess þarf að beita aðferðum forritunar, eins og lykkjum til að endurtaka aðgerðir, oft með einhverjum tilbrigðum, og skilyrðum til að ákvarða hvað gera skal út frá einhverjum forsendum: ef… þá… annars…(e. if… then… else…). Yfirleitt er forrit skrifað á forritunarmáli (e. programming language) sem fólk getur skilið. Dæmi um forritunarmál eru Scratch, Python og JavaScript. Þegar forrit er keyrt (framkvæmt) þá er forritunarmálið þýtt yfir á vélamál (e. machine language) sem tölvan skilur.

Stærðfræðinám ætti að leiða til þess að nemendur öðlist aukna getu til þess að skapa og tjá hluti. Það getur til dæmis verið gagnlegt að geta

• brotið verkefni niður í smærri einingar,
• skoðað stóru myndina fyrst (smærri atriði má síðan skoða síðar),
• valið gagnlegar leiðir til þess að skrásetja og vinna með gögn,
• sett fram tilgátur og alhæft,
• hugsað um og sett fram lausn sem aðrir skilja og geta farið eftir.

Glöggir lesendur sjá tengingu þessara atriða við þá meginþætti reiknihugsunar sem nefndir voru fyrr í þessari grein.

Lokaorð

Þótt hugtökin reiknihugsun og forritun hafi fyrst nú fest sig í sessi í íslenskri aðalnámskrá þá hafa þau verið hluti af lífi fólks í íslensku samfélagi um nokkurt skeið. Í þessari grein höfum við leitast við að útskýra hvað reiknihugsun og forritun fela í sér og í þeim tilgangi rætt um reiknirit, lykkjur, breytur og skilyrði. Við gáfum tvö dæmi um verkefni sem eiga við ólík aldursstig grunnskólans.

Í nútímasamfélagi erum við umkringd tækjum sem reikna í gríð og erg og reiknirit stýra í auknum mæli þeim upplýsingum og fréttum sem okkur berast. Með því að átta sig betur á gangverki reiknirita – hvað þau reikna og hvernig – er stefnt að því að börn og ungmenni öðlist sterkari forsendur til að verða gagnrýnir neytendur upplýsinga og geti tekið virkan þátt í lýðræði. Reiknihugsun gegnir því enn veigameira hlutverki en áður. Samfélagi sem er annt um lýðræði ætti að vera annt um hlut reiknihugsunar í menntun barna og ungmenna.

Heimildir

Aðalnámskrá grunnskóla: Almennur hluti 2011: Greinasvið 2024.

Bocconi, S., Chioccariello, A., Kampylis, P., Dagienė, V., Wastiau, P., Engelhardt, K., Earp, J., Horvath, M. A., Jasutė, E., Malagoli, C., Masiulionytė-Dagienė, V. og Stupurienė, G. (2022). Reviewing computational thinking in compulsory education. State of play and practices in computing education. Publications Office of the European Union. https://doi.org/10.2760/126955

OECD. (2022). PISA 2022: Mathematics Framework. https://pisa2022-maths.oecd.org/ca/index.html

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.

Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35. https://doi.org/10.1145/1118178.1118215

---

---

Greinin var áður birt í Skólaþráðum, tímariti Samtaka áhugafólks um skólaþróun, þann 14. desember 2025: https://skolathraedir.is/2025/12/14/reiknirit-reiknihugsun-og-forritun-nyjar-aherslur-i-namskra/