Kristín Bjarnadóttir.
Ekki verður lengi rætt um þátt stærðfræðinnar í sögu vestrænnar menningar án þess að nafninu Evklíð bregði fyrir. Hver var Evklíð? Í raun er lítið vitað um manninn. Hann bjó í Alexandríu, grískri nýlenduborg sem Alexander mikli stofnaði árið 325 f.Kr. við ósa Nílar í Egyptalandi. Talið er að Evklíð hafi verið uppi á tímabilinu frá um 325–320 fram til 280–265 f.Kr.
Evklíð safnaði saman allri stærðfræði sem þekkt var á hans tímum í eina bók, sem nefndist á grísku Stoikheîa (στοιχείο, e. Elements), en nefna mætti Frumþætti á íslensku. Ritið, sem var fullbúið um árið 300 f.Kr., skiptist í 13 bækur. Það varð ein kunnasta stærðfræðibók sögunnar, þýdd á mörg tungumál (ekki þó á íslensku enn sem komið er), rædd og rýnd, og kennslubækur voru sniðnar eftir henni.

Talið er líklegt að Evklíð hafi reynt að sníða bók sína sem einfaldasta og skýrasta, svo að textinn yrði hverjum manni ljós. Þó er sagt að konungurinn Ptolemeus I, eftirmaður Alexanders mikla, hafi kvartað við Evklíð yfir að hann skildi ekki efni bókarinnar. Evklíð hafi þá sagt hin fleygu orð: „Það er engin konungleg leið að rúmfræðinni, herra minn“.
Efni Frumþátta vindur fram með afleiðslu (e. deduction), þannig að sannanir og reglur eru leiddar af frumhugtökum og frumforsendum. Reglur, sem þannig hafa fengist, verða síðan forsendur annarra reglna, einfaldra og flókinna.
Afleiðslukerfi Evklíðs hefst á 10 frumforsendum, forsendum sem eru ósannaðar en óumdeildar. Þær eru oft nefndar frumsendur. Allar aðrar setningar eru leiddar af þeim. Fimm fyrstu frumsendurnar eru almennar og varða alla stærðfræði en hinar fimm seinni fjalla um rúmfræðina sérstaklega.
Almennu frumsendurnar eru:
1. Séu tveir hlutir báðir jafnir þriðja hlut þá eru þeir líka jafnir hvor öðrum.
2. Sé jafnmiklu bætt við tvo jafna hluti verða útkomurnar jafnar.
3. Sé jafnmikið tekið af tveim jöfnum hlutum verða útkomurnar jafnar.
4. Hlutir sem fylla sama rúm eru jafnir.
5. Heild er stærri en hluti hennar.
Rúmfræðilegu frumsendurnar eru:
1. Frá hvaða punkti sem er má draga beina línu í hvaða punkt sem er.
2. Strik af endanlegri lengd má framlengja í beina línu.
3. Hægt er að draga hring með hvaða fjarlægð sem er fyrir radíus og hvaða punkt sem er fyrir miðju.
4. Öll rétt horn eru jafn stór.
5. Ef strik sker tvær línur og innri hornin á aðra hlið þess eru samtals minni en tvö rétt horn þá skerast línurnar tvær þeim megin við strikið ef þær eru framlengdar ótakmarkað.
(Þýðandi Atli Harðarson, 2001).
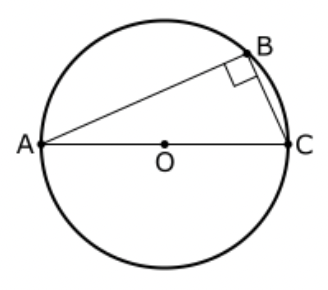
Evklíð var þó ekki fyrstur manna til að byggja upp afleiðslukerfi, enda er rit hans að mestu safn þess sem áður var þekkt. Löngu áður hafði Þales frá Míletos (624 – 547 f.Kr.) sett rúmfræði fram í afleiðslukerfi og sýnt fram á að sé þríhyrningur innritaður í hring þannig að eitt horn hans sé á hringferlinum og mótlæg hlið hornsins miðstrengur hringsins, þá er hornið á hringferlinum rétt horn. Reglan er nefnd Þalesar regla.
Krókaleið Frumþátta til vorra tíma
Ríki Alexanders mikla stóð ekki lengi. Um árið 270 f.Kr. hafði það liðast í sundur. Um síðir hnignaði einnig nýsköpun á sviði stærðfræði í gríska menningarheiminum. Íbúar Rómar, Rómverjar, tóku að þenja út ríki sitt yfir Ítalíuskagann. Þeir höfðu hafið frekari útþenslu til suðurs þegar stærðfræðingurinn Arkimedes féll fyrir hendi rómversks hermanns í Sýrakúsu á Sikiley árið 212 f.Kr. Það gerðist í annarri púnversku styrjöldinni milli Rómverja og íbúa Karþagó, borgar við sunnanvert Miðjarðarhaf þar sem nú er Túnis.
Rómverjar réðu lögum og lofum við Miðjarðarhaf þar til Rómaveldi klofnaði í austrómverskan og vestrómverskan hluta. Vestrómverska ríkið féll endanlega árið 476 e.Kr. Ólæsir germanskir þjóðflokkar lögðu undir sig meginhluta Evrópu. Forn stærðfræðirit týndust og gleymdust í Vestur-Evrópu en voru að nokkru varðveitt í austrómverska ríkinu, Býsans, og í Miðausturlöndum.
Böþíus, sem uppi var um 500 e.Kr., er talinn hafa þýtt á latínu bók eftir Níkómakkos frá Gerasa sem var uppi um 100 e.Kr. Borgin Gerasa var þá í Sýrlandi en er nú í Jórdaníu. Bók Níkómakkosar var rituð á grísku og nefndist Frumatriði talnafræðinnar (gr. Arithmētikē eisagōgē). Þýðing Böþíusar var notuð til kennslu í dómkirkjuskólum eftir að menntastarfi rómversk-kaþólsku kirkjunnar óx ásmegin.
Frá níundu til tólftu aldar var texti Böþíusar meginkennsluefnið í stærðfræði. Þar var fjallað um talnaspeki, sléttar tölur og oddatölur, prímtölur og samsettar tölur, ítarlega flokkun á hlutföllum og mismunandi meðaltöl: hreint meðaltal (e. arithmetic mean), faldmeðaltal (e. geometric mean) og þýtt meðaltal (e. harmonic mean). Námsefnið í rúmfræði fólst í skilgreiningum, frumsendum og setningum úr I. og II. bók Frumþátta, nokkrum sönnunum og flatarmálsreglum. Þannig bárust Frumþættir smám saman til baka til Evrópu, fyrst í brotum úr grísku en síðar í heilsteyptri þýðingu úr arabísku.
Hinn hluti Rómaríkis varð austrómverska ríkið, Býsansríkið eða Miklagarðsríkið, þar sem rétttrúnaðarkirkjan ríkti. Býsansríkið stóð fram til 1453. Miðstöð þess var í Konstantínópel, Miklagarði. Þar geymdist gríski stærðfræðiarfurinn og um síðir barst hann til Húss viskunnar í kalífaríki múslima í Bagdad. Hús viskunnar, Bayt Ul-Hikma, var bókasafn og þýðingarsetur í Bagdad, stofnað á tímum Abbassida kalífaveldisins. Bókasafnið geymdi meðal annars þýðingar á fræðiritum sem voru upphaflega rituð á grísku og sanskrít. Bókasafnið skapaði því hagstæð skilyrði fyrir samruna austrænnar og vestrænnar menningar.
Á tímabilinu 700 – 900 e.Kr. höfðu þjóðir Miðausturlanda þýtt grísk rit á arabísku, meðal annars Frumþætti Evklíðs, en einnig rit Arkimedesar og fleiri grískra höfunda, og bætt við þau. Framhald sögunnar er síðan að forngrísku ritin í arabískum búningi tóku að berast til Evrópu í gegnum Spán eftir að kalífaveldinu tók að hnigna þar á 12 öld. Latneskar þýðingar á grísku og arabísku ritunum ollu mikilli vakningu Evrópu í stærðfræðilegum efnum, og hún hefur staðið allar götur síðan.
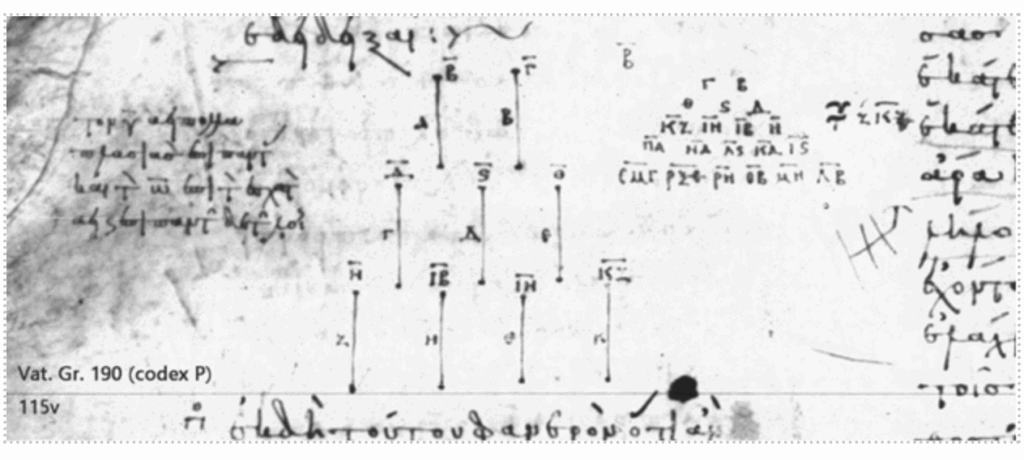
Um efni Frumþátta var fjallað á ólíka vegu eftir menningarsamhengi. Mynd 3 sýnir hluta úr handriti á grísku frá 9. öld um setningu 2 í bók VIII, sem segir frá hlutfallinu 3/2 milli talnanna 8 – 12 – 18 – 27.
Umfjöllun um setningu 2 í bók VIII er einnig að finna í ritgerðinni Algorismus, sem talin er þýdd á íslensku úr latínu um miðja 13. öld, en handritið AM 736 III 4to er talið ritað um 1550. Þar birtast sömu tölur í talnaspekilegum búningi, lítt tengdar afleiðslu. Tölurnar 8 – 12 – 18 – 27 eru tengdar við höfuðskepnurnar eld – loft – vatn – jörð (lat. ignis – aer – aqua – terra).
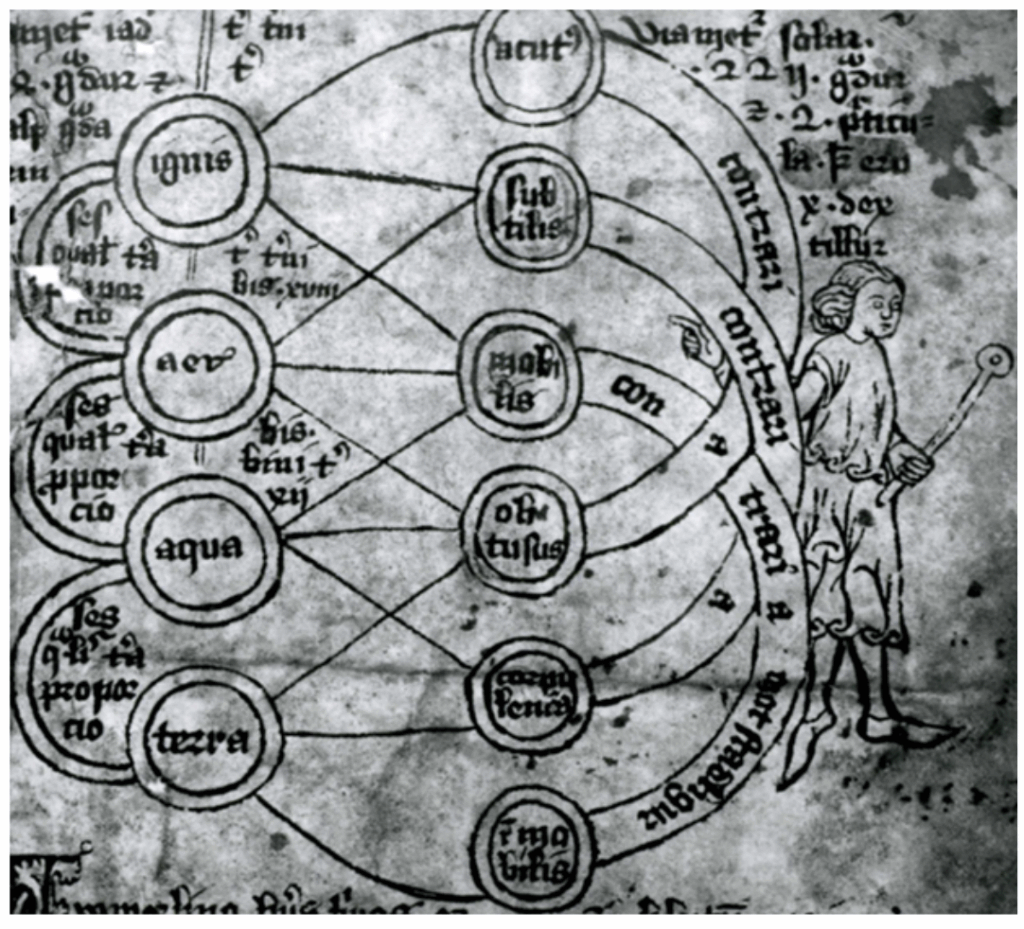
Ofan við hringinn á Mynd 4, þar sem stendur ignis (eldur) stendur „tres trium tres (þrisvar þrír þrisvar)“ (27), við hringinn með aer (loft) stendur „tres trium bis xviii (þrisvar þrír tvisvar)“ (18), við aqua (vatn) má sjá „bis bini tres xii (tvisvar tveir þrisvar)“ (12). Í hringjunum sex á miðri mynd má sjá tilvísanir í geðslag fólks: acutus, subtilis, mobilis, obtusus, corpulus, immobilis (lauslega þýtt: ákafur, viðkvæmur, hviklyndur, deigur/daufur, þunglamalegur, óbifanlegur). Lesandanum er látið eftir að hugleiða merkingu þessara orða um mannlega eiginleika og skoða tengsl þeirra á myndinni við frumefnin eld, loft, vatn og jörð.
Kennslubækur í rúmfræði fyrir framhaldsskóla voru gjarnan sniðnar eftir Frumþáttum langt fram á tuttugustu öld. Nefna má Rúmfræði eftir Julius Petersen sem kennd var við Menntaskólann í Reykjavík og forvera hans, Lærða skólann, í um eitt hundrað ár (um 1870 – um 1970). Þótt bókin hafi þótt nokkuð stirfin, má segja að uppbygging textans með afleiðsluaðferð og afleiðslukerfi hafi lagt grundvöll að þjálfun í rökleiðslu sem er eitt af meginviðfangsefnum stærðfræðináms.
Heimildir og frekara lesefni
Atli Harðarson. (2001). Fimm kaflar um sögu rúmfræðinnar. https://atlivh.com/textar/stae/fimm_kaflar_um_sogu_rumfraedinnar.pdf
Jón Þorvarðarson (2005). Og ég skal hreyfa jörðina. Reykjavík, STÆ ehf.
Kristín Bjarnadóttir. (2016, 29. apríl). Hvernig barst þekking um stærðfræði á milli menningarþjóða á miðöldum og hver var þáttur Araba í því? Vísindavefurinn. https://visindavefur.is/svar.php?id=72148
Kristín Bjarnadóttir & Bjarni V. Halldórsson (2021). Algorismus: Hindu-Arabic Arithmetic in GKS 1812 4to. Í Gunnar Harðarson, Christian Etheridge, Guðrún Nordal & Svanhildur Óskarsdóttir (ritstj.), A World in Fragments, Studies on the Encyclopedic Manuscript GKS 1812 4to. Reykjavík, Árnastofnun.
Kristín Bjarnadóttir, Dirk De Bock, & João Bosco Pitombeira de Carvalho (2024). Chapter 23. The origin and evolution of the concept of mathematics curriculum. Í M. A. (Ken)Clements, Berinderjeet Kaur, Thomas Lowrie, Vilma Mesa, & Johan Prytz (ritstj.), Fourth International Handbook of Mathematics Education. Springer.

Kristín Bjarnadóttir, fyrrum prófessor emerita við Háskóla Íslands