Ingólfur Gíslason
Verkefnið Vélmenni á talnalínu er að finna í myndbandinu Negative numbers in context.
Tilgangur verkefnisins í myndbandinu er að auka skilning nemenda á neikvæðum tölum. Neikvæðum tölum er gefinn sá tilgangur að vera hluti af stærðfræðilegu líkani af staðsetningu og færslu í tvær mismunandi áttir.
Skoðum fyrstu útfærsluna á mynd 1.
 犀利士
犀利士
dth=“891″ height=“464″ />
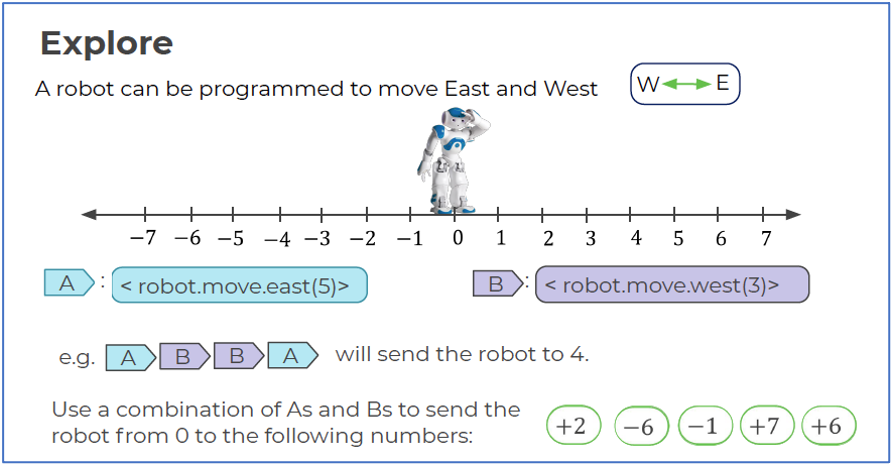
Mynd 1.
Gefa má tvær skipanir, A og B. A færir vélmennið í austur (til hægri) um 5 og B færir
vélmennið í vestur (til vinstri) um 3. Nemendur eru beðnir að senda vélmennið á nokkrar
tilteknar tölur frá byrjunarreitnum, 0. Í sjálfu sér er verkefnið nokkuð opið, því það er hægt
að fara ólíkar leiðir við að leysa það og finna má margar mismunandi lausnir. Til dæmis má
komast á 4 með ABAB (5-3+5-3) og AABB (5+5-3-3) og AABBBAABBBAABBBAABBB (og ótal
fleiri leiðum). Það væri kannski ekki vitlaust að skjóta inn spurningu um þetta: Skiptir röð
skipana einhverju máli? Einnig má velta fyrir sér hversu margar ólíkar leiðir séu færar til að
komast á tilteknar tölur eða hvaða tölur við getum komist á ef við megum bara nota þrjú A
og tvö B. Hér í framhaldinu verður því lýst hvernig hægt er að opna og útvíkka verkefnið enn
frekar og gera úr því verðugra verkefni, nokkuð djúpa stærðfræðilega rannsókn.
Eiginleikar
Við byrjum á að skrá: hverjir eru eiginleikar verkefnisins? Hér eru alltaf óteljandi margir
möguleikar og það er enginn einn réttur listi. Tilgangurinn með slíkum lista er að við getum skoðað hann síðar og spurt hvað ef ekki? Hvað ef einhver eiginleiki er ekki svona? Hvað ef
við breytum einum eða fleiri eiginleikum?
- Við ferðumst eftir talnalínu,
- við fáum tvo möguleika á að færa vélmennið,
- við megum fara 5 til hægri og 3 til vinstri,
- tölurnar 5 og 3 eru báðar oddatölur,
- tölurnar 5 og 3 eru báðar frumtölur,
- tölurnar 5 og 3 hafa engan sameiginlegan frumþátt, með öðrum orðum er engin tala
fyrir utan 1 sem gengur upp í báðar tölurnar.
Það er hægt að halda áfram og finna fleiri eiginleika. En hér eru nokkrar hugmyndir um það
hvert má fara með verkefnið:
- Hvað ef við ferðumst ekki á talnalínu heldur í hnitakerfi, í tvívídd? Megum við þá fara
í 4 áttir (eða fleiri), norður, austur, suður, vestur. Hvað ef við höfum það í þrívídd?
Hvað ef við ferðumst á kúluyfirborði? - Hvað ef við myndum bara fá einn möguleika á færslu? Eða þrjá? Eða fleiri?
- Hvað ef við myndum mega hoppa með margföldun eða deilingu eða á einhvern
annan hátt? - Hvað ef báðar tölurnar væru sléttar tölur?
- Hvað ef tölurnar hafa sameiginlegan frumþátt?
- Hvað ef nemendur fá að velja tölurnar?
Hér mætti líka halda áfram.
Tilgátur og alhæfingar
Upprunalega verkefnið um vélmennið, sem kynnt var í inngangi þessarar greinar, skortir
einn mikilvægan eiginleika til að geta talist stærðfræðilegt verkefni í raun og veru: tækifæri
til þess að alhæfa. Að alhæfa í stærðfræði þýðir að finna einhverja almenna reglu, eitthvað
sem er alltaf satt, eða alltaf satt þegar einhver tiltekin skilyrði eru til staðar. Þess vegna er
áhugavert að í myndbandinu sem fylgir verkefninu fylgir ein spurning í viðbót: Getið þið
fundið heila tölu sem vélmennið kemst ekki til? Því miður vantar oft sambærilega spurningu í
verkefni í kennslubókum, spurningu sem kallar á alhæfingu og stærðfræðilega hugsun. Ef þið
hafið lagt ykkur fram um að glíma við verkefnið þá ættuð þið að geta sett fram tilgátu:
Vélmennið kemst hvert sem er.
Röksemdir og sannanir
Það er engin heil tala til sem vélmennið kemst ekki á. Þetta má rökstyðja á marga vegu.
Lausnir sem hafa komið fram þegar verkefnið hefur verið sett fyrir kennaranema ganga
margar út á að finna nokkrar tölur í röð sem hægt er að komast á, og vinna út frá því. Til
dæmis er hægt að sjá að:
- 1 = AABBB (5 + 5 – 3 – 3 – 3 = 10 – 9 = 1)
- 2 = AB
- 3 = AAABBBB
- 4 = ABBA
- 5 = A
Nú höfum við fimm tölur í röð og þá er hægt að fá næstu fimm tölur með því að bæta 5 við
hverja þeirra (með því að bæta við A). Sem dæmi er 6 = 5 + 1 = AAABBB (einu A bætt framan
við lausnina fyrir 1). Þannig getum við fært okkur áfram upp eftir talnalínunni: Við höfum
tölurnar 1, 2, 3, 4 og 5 og með því að nota A (bæta við 5) út frá hverri þeirra fást næstu fimm
tölur, 6, 7, 8, 9 og 10, og þannig má halda áfram koll af kolli.
Við nánari umhugsun og skoðun getum við einfaldað þessi rök. Fyrst við getum komist í 1, þá
getum við komist á hvaða jákvæðu tölu sem er. Við getum endurtekið 1 (AABBB) eins oft og
þarf til komast þangað sem við viljum. Þá fást stundum óþarflegar langar leiðir, en þær virka!
Á sama hátt vitum við að -1 = ABB, og þá er hægt að endurtaka ABB eins oft og þarf til að fá
hvaða neikvæðu tölu sem er. Til að komast í töluna 456 notum við AABBB 456 sinnum í röð.
Með því að nota algebrulegan rithátt getum við sagt þetta svona: Það að komast á jákvæðu
töluna n, þýðir að finna tölur x og y þannig að n = 5x – 3y. En við vitum að
1 = 5 ∙ 2 – 3 ∙ 3 og þá er n = n(5 ∙ 2 – 3 ∙ 3) = 2n ∙ 5 – 3n ∙ 3. Þetta segir okkur þá til
dæmis að til þess að komast í töluna 456 getum við notað 2 ∙ 456 = 912 sinnum A, og 3 ∙ 456 = 1368 sinnum B.
Myndræn leið til að sjá þetta:
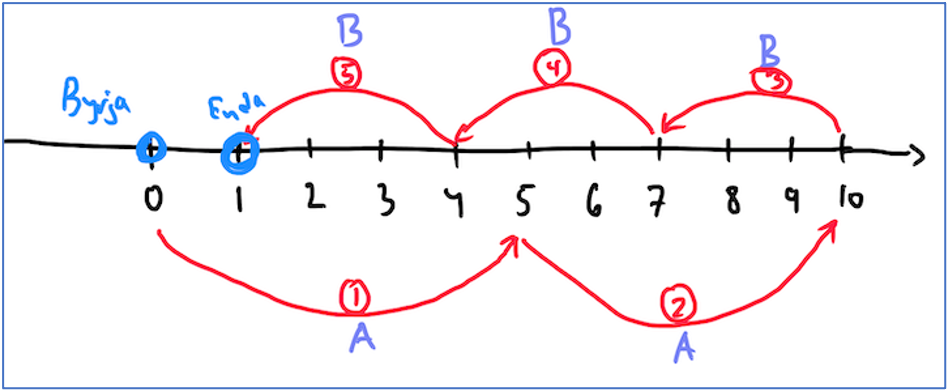
Mynd 2.
Á mynd 2 sést hvernig hægt er að komast á töluna 1 með leiðinni AABBB. Það má gjarnan spá í það hvort röðin á skipununum (A og B) skipti máli. Á mynd 3 sjáum við almenna tilfellið, almenn rök fyrir því að það megi alltaf komast í tölu sem er einum hærri en talan sem við höfum nú þegar komist á. Ég nota hér bókstafinn n til þess að tákna hvaða tölu sem er. Sú tala sem er einum hærri en n er þá talan n + 1 og svo koll af kolli.
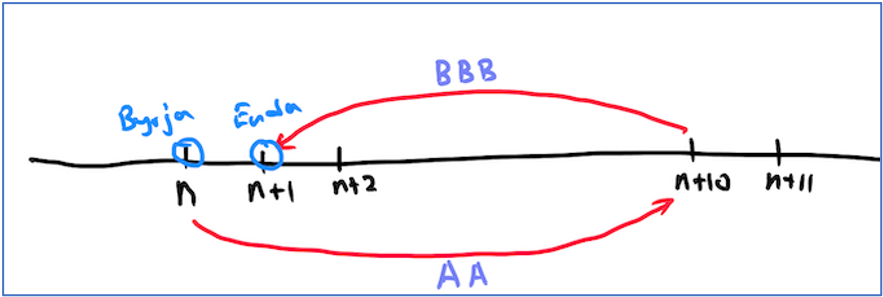
Mynd 3.
Í fræðilegri stærðfræði eru röksemdarfærslur á borð við þessa nefndar sannanir með þrepun
eða þrepasannanir. Í þeirri útgáfu sem hér er um að ræða þá er sýnt fram á tvo hluti:
- að reglan gildi um töluna 1 (hægt er að komast á töluna 1),
- að ef reglan gildir um einhverja tölu þá gildir hún líka um næstu tölu þar á eftir (ef hægt er að komast á einhverja tölu þá er hægt að komast á næstu tölu á eftir í talnaröðinni).
Ef þetta tvennt er satt, þá gildir reglan um allar heilar jákvæðar tölur. Í okkar tilfelli er reglan
sú að „vélmennið kemst í töluna“.
Og hvað? Af hverju að fjalla um þetta?
Umfjöllunin er sett fram hér til að sýna fram á að verkefni sem hæfir grunnskólanemum getur haft mikla þýðingu og boðið upp á djúpa stærðfræðilega hugsun. Ungt fólk er fullfært um að finna þau rök sem kynnt hafa verið hér að ofan ef þau fá hvatningu og ögrandi spurningar frá kennara. Þau geta sett rökin fram og sannfærst af þeim þó að þau þurfi ekki að setja þau formlega fram eða að læra formlega um þrepasannanir. Þrepasannanir eru annars venjulega ekki kynntar fólki fyrr en á síðasta ári í framhaldsskóla og þá yfirleitt einungis þeim sem eru á náttúruvísindabraut eða annarri braut sem inniheldur mikla stærðfræði. Þær eru svo viðfangsefni í háskólanámi í stærðfræði og eru mikilvægar í tölvunarfræði.
Hver er stærðfræðilegur kjarni verkefnisins?
Greiningin á verkefninu leiðir í ljós að ef hægt er að komast á töluna 1, þá er hægt að komast hvert sem er á jákvæða hluta talnalínunnar (og eins, ef hægt er að komast í -1, þá er hægt að komast hvert sem er á neikvæða hluta talnalínunnar). En hvaða eiginleikar talnanna 5 og -3 gera þetta mögulegt? Ein leið til að opna verkefnið er að stinga upp á að prófa aðrar tölur, annaðhvort frjálst eða að gefa tilteknar tölur. Þegar verkefnið var sett fyrir kennaranema haustin 2021 og 2022 voru gefnar tölurnar 15 og -18, það er að segja að skipanir vélmennis urðu A: 15 skref í austur og B: 18 skref í vestur. Ástæðan er sú að þessar tölur hafa sameiginlegan þátt, 3. Hvaða áhrif skyldi það hafa? Jú, þetta veldur því að einungis er hægt að komast í tölur sem eru margfeldi af 3. Það er að segja, allar skrefastærðir verða í þrisvar sinnum töflunni og ef vélmennið byrjar í 0 þá kemst það ekki út fyrir tölurnar í þeirri töflu. Við þessa útvíkkun var eiginleiki talnanna 5 og -3 kannaður og honum breytt: Hvað ef tölurnar hafa sameiginlegan frumþátt? Og verkefnið sett fram með tveimur tilteknum tölum með nýja eiginleikanum. Í næstu spurningu þar á eftir var nemendum sagt að velja sjálfir skrefastærðir og að setja fram tilgátu (sem er líka alhæfing) um það hvaða eiginleika þrepastærðirnar þurfa að hafa til þess að vélmennið komist hvert sem er. Þar með hefur verkefnið verið opnað mjög mikið: Nemendur velja sjálfir tölur til að prófa og þeir fást við að alhæfa og rökstyðja í samhengi sem er stærðfræðilega djúpt og mikilvægt.
Í raun og veru nálgast nemendur með þessu fræga reglu sem nefnist jafna Bezout. Það er sú staðreynd að ef stærsti sameiginlegi þáttur tveggja jákvæðra heilla talna a og b er talan d, þá er hægt að finna heilar tölur x og y þannig að d = ax + by. En, líkt og ekki þarf nauðsynlega að ræða þrepasannanir þá er heldur alls ekki nauðsynlegt að ræða jöfnu Bezout sem slíka eða kynna hana sem reglu til að læra.
Þegar ég útvíkkaði verkefnið valdi ég að taka alhæfinguna sem bent var á í verkefninu (Er hægt að komast hvert sem er?) og gera hana að nánara skoðunarefni með því að kanna hvað gerist ef við breytum eiginleikum talnanna tveggja sem gefnar voru sem skrefastærð. Það væri líka hægt að fara í aðrar áttir eins og kemur fram í „hvað ef“ listanum.
Eitt dæmi um verkefni er eftirfarandi:
Vélmennin Robbi og Tóta eru stödd í upphafspunkti hnitakerfis (0,0). Hægt er að gefa fjórar
skipanir fyrir hvert vélmenni, samkvæmt eftirfarandi töflu:
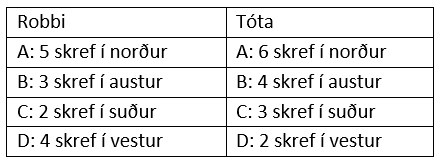
Spurningar:
- Tóta færði sig samkvæmt skipununum ABCD og endaði þar með í punktinum (2, 3).
Kemst Robbi þangað? Hvernig eða hvers vegna ekki? - Robbi færði sig samkvæmt skipunum sínum ABCD og endaði þar með í punktinum (-1,3).
Kemst Tóta þangað? Hvernig eða hvers vegna ekki? - Lýstu mismunandi möguleikum Robba og Tótu til að komast um í hnitakerfinu. Hvert
kemst Robbi? Hvert kemst Tóta? - Nú á að hanna skipanir fyrir tvö vélmenni með sama hætti (segja hve mörg skref í hverja
átt þau mega fara). Þau byrja bæði á (0,0) en mega svo aldrei mætast á neinum öðrum stað.
Finnið leiðir til að gera þetta.
Hér má halda áfram með fleiri spurningar sem snúast um það hvers konar mengi af skipunum virka til að komast hvert sem er og hver virka ekki.
Samantekt: Að opna og útvíkka stærðfræðiverkefni
Hér hefur verið reynt að gefa innsýn í það hvernig vinna má með gefið stærðfræðiverkefni
og gera úr því verðugt verkefni sem reynir á stærðfræðilega hugsun. Í verðugu stærðfræðiverkefni felst að gera tilgátur sem fela í sér alhæfingar og að rökstyðja þær.
Ein leið til þess að opna og útvíkka verkefni er að:
- Gera lista yfir eiginleika verkefnis og þeirra stærðfræðilegu hluta sem eru í því.
- Fara yfir listann og breyta eiginleikunum: Hvað ef (ekki) …?
- Skoða útkomur gegnum alhæfingar: Er þetta alltaf svona? Hvaða eiginleikum má
breyta þannig að það gildi samt alltaf það sama? Er hægt að beina athygli nemenda
að þessum hlutum með vel völdum tölum, formum eða fyrirbærum? - Athuga að meginatriðið sé röksemdir og tengsl frekar en eingöngu reikningar.
Þannig er hægt að nýta fyrirliggjandi kennslubækur og verkefni til þess að stuðla að meiri
stærðfræðihugsun.
Ingólfur Gíslason er aðjunkt við Menntavísindasvið Háskóla Íslands
















