Jóhann Örn Sigurjónsson.
Þessi grein byggir á erindi mínu á námstefnu Flatar sem haldin var á 30 ára afmæli samtakanna þann 4. mars 2023. Ég segi í stuttu máli frá hluta niðurstaðna úr doktorsverkefni mínu um hugræna virkjun í stærðfræðikennslu á Íslandi (Jóhann Örn Sigurjónsson, 2023). Ég leitast við að útskýra hvað hugræn virkjun er, bæði með samlíkingunni við kennslu til skilnings og með fróðleik um hvað tiltekinn matsrammi metur til gæða í hugrænni virkjun. Þá tek ég nokkur dæmi um krefjandi verkefni í stærðfræði sem skapa góðan jarðveg til þess að virkja hugsun nemenda – stuðla að hugrænni virkjun á háu stigi.
Fyrir mörgum kann að virðast nýstárlegt að tala um þátt í gæðum kennslu sem kallast hugræn virkjun. Rannsakendur hafa gjarnan skipt gæðum kennslu í þrjá yfirþætti: hugræna virkjun, stuðning við nám og bekkjarstjórnun (Praetorius, Klieme, Herbert og Pinger, 2018). Rétt eins og kennari stýrir ekki beinlínis bekk með handafli, þá virkjar kennari ekki hugsun nemenda með því að teygja sig inn í huga þeirra og smella á rofa undir höfuðkúpunni. Hugræn virkjun er því gjarnan hugsuð út frá svonefndu bjóða-nota líkani (Weingartner, 2021). Samkvæmt bjóða-nota líkaninu þá býður kennari nemendum tækifæri til hugrænnar virkjunar. Hugræn virkni nemenda byggir síðan á því hvernig nemendur nota þessi tækifæri. Tækifæri til hugrænnar virkjunar má í stuttu máli skilgreina út frá tveimur ákvörðunum kennarans:
● Hlutlæg tækifæri til hugrænnar virkjunar: Val kennarans á krefjandi verkefnum.
● Útfærð tækifæri til hugrænnar virkjunar: Útfærsla á verkefnum í kennslustund.
Um val verkefna og ólíkar tegundir þeirra eftir vitsmunalegum kröfum eru til viðmið sem kennarar geta hagnýtt sér (sjá t.d., Jóhann Örn Sigurjónsson og Berglind Gísladóttir, 2020). Í niðurstöðum sem hér eru kynntar er áherslan á hið síðarnefnda, þ.e. hvernig verkefni eru útfærð í kennslu í samskiptum við nemendur í kennslustund.
Gögn rannsóknarinnar eru hluti af stærra gagnasafni. Rannsóknarsetrið Quality in Nordic Teaching (QUINT) hefur síðan 2018 safnað myndbandsupptökum úr kennslustundum í 8. bekk af öllum Norðurlöndum. Í þessari grein verður byggt á gögnum úr kennslustundum í stærðfræði á Íslandi. Teknar voru upp 34 kennslustundir í stærðfræði frá tíu kennurum, þrjár til fjórar kennslustundir frá hverjum kennara. Fimm þátttökuskólar voru af höfuðborgarsvæðinu og fimm af landsbyggðinni. Til að varðveita nafnleysi þátttakenda eru notuð gervinöfn í niðurstöðum.
Gögnin voru greind með greiningarrammanum PLATO (Grossman, 2015). Í PLATO eru í heild tólf þættir, þar sem fyrir hvert 15 mínútna myndskeið er hver þáttur metinn á fjögurra þrepa kvarða. Byggt er á vísbendingum í myndbandsgögnunum þar sem á 1. þrepi eru litlar eða engar vísbendingar, en á 4. þrepi eru sterkar og stöðugar vísbendingar. Tveir PLATO þættir tengjast yfirþættinum hugrænni virkjun: vitsmunaleg áskorun og samræður í kennslustund. Á myndum 1 og 2 má sjá stytt greiningarviðmið fyrir þessa tvo þætti.

Mynd 1. Stytt PLATO viðmið fyrir vitsmunalega áskorun (e. intellectual challenge, IC)

Mynd 2. Stytt PLATO viðmið fyrir samræður í skólastofunni (e. classroom discourse, CD)
Þess skal geta að spurningar og athugasemdir kennarans geta orðið til að auka á vitsmunalega áskorun verkefna eða draga úr henni. Mat á vitsmunalegri áskorun er þá hækkað eða lækkað um eitt þrep eftir því hvort kennarinn eykur eða minnkar kröfur fyrir úrlausn verkefnis.
Niðurstöður og innsýn í tvo hópa
Á mynd 3 má sjá dreifingu myndskeiða í hugrænni virkjun eftir kennurum. Út frá niðurstöðum þeirra kennslustunda sem greindar voru má skipta þátttökukennurum í þrjá hópa. Í hópi A eru kennarar þar sem dæmi voru um að þættirnir vitsmunaleg áskorun og samræður í kennslustund væru metnir á 4. þrepi. Í hópi B eru kennarar þar sem þessir þættir voru hæst metnir á 3. þrepi. Í hópi C eru loks kennarar þar sem þættir tengdir hugrænni virkjun voru metnir á 1. eða 2. þrepi í öllum myndskeiðum kennslustunda þeirra.
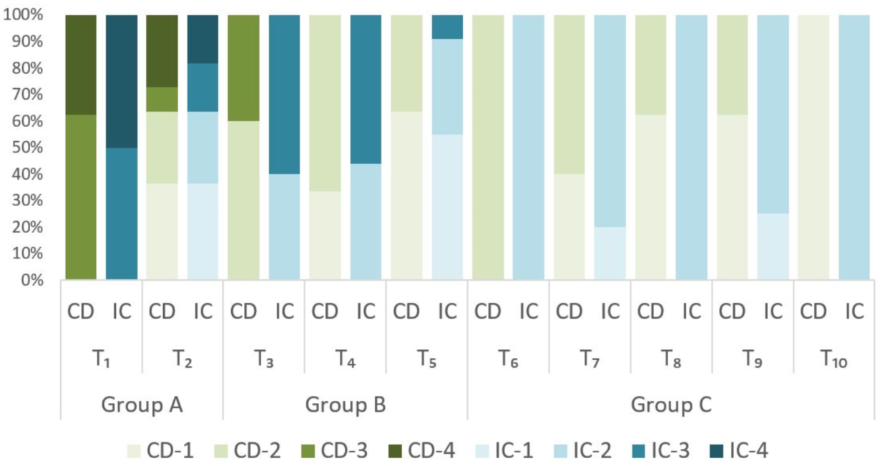
Mynd 3. Dreifing myndskeiða í hugrænni virkjun eftir kennurum.
Í hópi A voru tveir kennarar, T1 og T2. Í kennslustundum kennarans T1 voru tekin fyrir verkefni í líkindafræði sem nemendur unnu saman í pörum. Meðal verkefna voru tilraunir nemenda með teningakast þar sem bornar voru saman tilraunalíkur og fræðilegar líkur. Kennarinn hafði bæði stuttlega beina kennslu til alls hópsins og gekk á milli á meðan nemendur köstuðu teningum og skráðu niðurstöður. Í samskiptum við nemendur spurði kennarinn þá gjarnan spurninga og leiðbeindi þeim þannig við að útskýra hugsun sína fyrir hvert öðru:
Kennari: Hverjar eru líkurnar á því að fá fimm ef þú kastar teningi?
Arnar: Einn á móti sex.
Kennari: Einn á móti sex. Hversu oft ætti ég að fá fimm ef ég kasta teningi 30 sinnum?
Arnar: 30 sinnum, er það ekki… fimm?
Kennari: Fimm sinnum. Af hverju? ⬅️
Arnar: Nei, sex sinnum, af því að fimm sinnum sex er 30.
Kennari: Ert þú sammála því? Mhm. Ok.
Beta: Ég skil ekki neitt!
Kennari: Arnar, getur þú útskýrt fyrir Betu? ⬅️
Örvarnar ⬅️ sýna vísbendingar um að kennarinn auki á vitsmunalega áskorun. Kennarinn spyr af hverju nemandi hefur tiltekna tilgátu og biður þannig um rökstuðning. Þá biður kennarinn hinn nemandann um að leggja mat á þetta og leiðbeinir loks um að útskýra hugsun sína fyrir bekkjarfélaga sínum. T2 viðhafði sams konar útfærslu verkefna í algebru, meðal annars með námsleiknum 24 sem verður sagt nánar frá síðar.
Í hópi C voru fimm kennarar, T6 til T10. Í kennslustundum þeirra unnu nemendur nánast eingöngu einir og „á eigin hraða“. Því unnu nemendur allajafna ekki sömu verkefni á sama tíma og var ekki leiðbeint að vinna saman sem gerði það að verkum að samræða var metin á lægri þrepum. Kennarinn gekk gjarnan um og aðstoðaði einstaklingslega en lítið sem ekkert var um kennslu til alls hópsins samtímis. Í aðstoð sinni við nemendur var gjarnan dregið úr áskorun verkefnanna, til dæmis með lokuðum spurningum eða með því að segja nemendum lausn eða lausnaleið. Í eftirfarandi dæmi bað nemandi um aðstoð við að búa til formúlu fyrir mn og reikna m80 þar sem myndrænt talnamynstur gaf m1 = 5, m2 = 9, m3 = 13 (eins og á mynd 4).
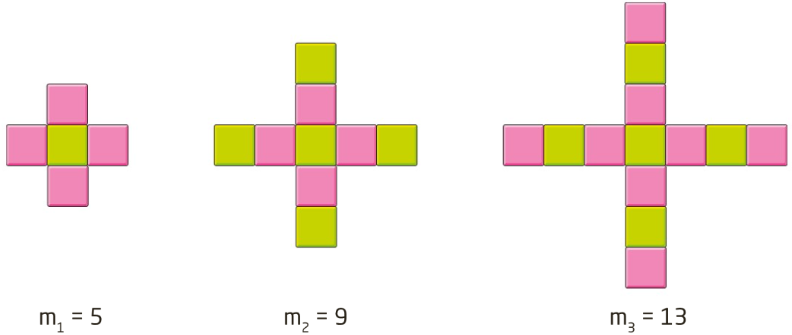
Mynd 4. Myndrænt talnamynstur þar sem í hverjum lið rununnar leggjast fjórar einingar við.
Kennari: Já, búðu til formúlu. Hvað breytist hérna á milli?
Nemandi: Einn plús…
Kennari: Það bætast við fjórir. Þá skrifar þú 4x. Ef þú tekur 4 af þessu, hvað verður mikið eftir?
Nemandi: Einn.
Kennari: Plús einn. Og svo er x-ið m-númerið.
Nemandi: Þannig að ef ég væri að finna 80, myndi ég þá bara gera fjórir…
Kennari: Fjórir sinnum 80 plús einn.
Nemandi: Ókei.
Kennari: Þetta er gert svona (kennari slær inn í reiknivél nemandans) fjórir sinnum 80 plús einn.
Hér hefur kennarinn í raun leyst dæmið í heild án þess að nemandinn þyrfti að sýna fram á nokkurn skilning eða eigin hugsun. Það varð til þess að dregið var úr vitsmunalegri áskorun. Ekki fundust dæmi um að leitað væri eftir rökstuðningi nemanda eða að þeir útskýrðu hugsun sína líkt og sjá mátti í dæminu úr hópi A. Þó mátti hjá báðum hópum kennara finna verkefni sem gáfu tækifæri til þess að hugræn virkjun væri á háu stigi – til dæmis í hópi C með verkefninu á mynd 4. Hefði útfærsla kennarans á verkefninu verið á annan veg hefði með góðu móti mátt meta þætti hugrænnar virkjunar á efri þrepum.
Dæmi um krefjandi verkefni
Við lok erindis míns kynnti ég eftirfarandi fimm krefjandi verkefni sem geta hentað vel til kennslu með hugræna virkjun á háu stigi. Hér segi ég nánar frá þremur þeirra.
1. Námsleikurinn 24.
2. Frumtöludagsetningar.
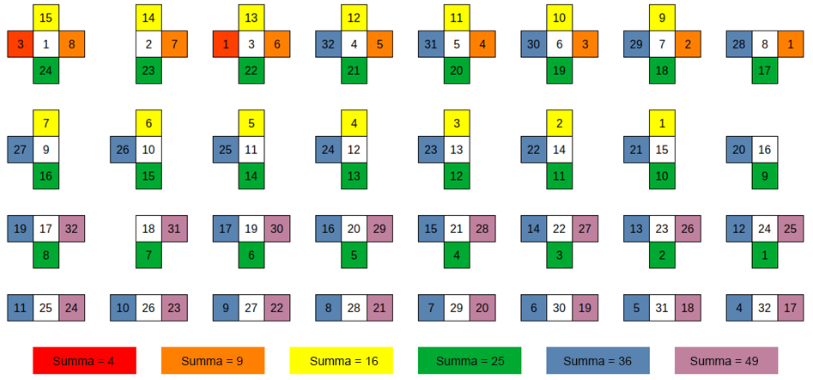
3. Röðun heiltalna 1-32 í hring þannig að summa aðliggjandi talnapara sé ferningstala.
4. Myndræn þáttun talna og annars stigs margliða.
5. Teningakast og reiknirit: Python forrit fyrir summu tveggja teninga og n teninga.
Leikurinn 24 gengur út á að af gefnu spjaldi með fjórum tölum á bilinu 1-9 á að nota sérhverja tölu einu sinni til að rita stæðu með grunnreikniaðgerðum sem hefur gildið 24. Spjald með tölunum 8, 7, 9 og 1 hefur til dæmis lausn með stæðunni (9−7+1)∙8. (Til er önnur lausn við þessu spjaldi.)
Þátttakendum voru gefin nokkur talnaspjöld til að leysa (sjá mynd 5). Gefnar voru þær upplýsingar að eitt spjaldið hafi enga lausn en ekki var gefið upp hvaða spjald það er. Af þessum fimm spjöldum sem hafa lausn er í spilinu sjálfu eitt þeirra merkt auðvelt, tvö eru miðlungs og tvö erfið.
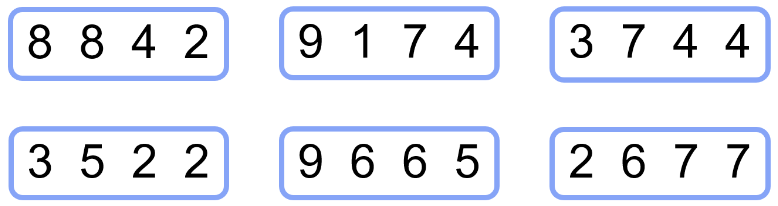
Mynd 5. Sex talnaspjöld fyrir leikinn 24. Eitt spjaldanna hefur enga lausn.
Það er áhugaverð staðreynd að ekki öll möguleg talnaspjöld hafi lausn, þó að í spilinu sem gefið er út af Suntex hafi öll 96 spjöldin lausn sem þar eru prentuð. Enn áhugaverðari staðreynd er að talnagildið 24 er ekki það gildi sem hefur hlutfallslega flestar lausnir ef öll möguleg talnaspjöld eru tekin með í reikninginn (fyrir ítarlegri greiningu á þessu má sjá grein Triplett, 2011).
Annað verkefni sem kynnt var þátttakendum á námstefnunni hafði að gera með svokallaðar frumtöludagsetningar. Í því átti að hugleiða eftirfarandi:
a) Ef litið er á dagsetninguna í dag sem átta (eða sjö) stafa tölu, rituð ddmmyyyy, þar sem
● dd er dagur,
● mm er mánuður
● yyyy er ártal
● …er talan ddmmyyyy frumtala? Hvað með daginn í gær?
b) Rannsakaðu og segðu til um líkurnar á því að gefin dagsetning á forminu ddmmyyyy sé frumtala.
c) Geta frumtöludagsetningar orðið tvo daga í röð?
d) Hverju breytir það í spurningum 2 og 3 ef notuð er átta stafa talan yyyymmdd?
Við að hugleiða þetta verkefni geta ýmis hugtök komið til kastanna, svo sem sléttar tölur og oddatölur, samsettar tölur og frumtölur, frumtölutvíburar, sem og ólík skilyrði eftir því hvort mánuðurinn er nýhafinn eða meira en 9 dagar liðnir af honum. Fyrir b-lið er ef til vill ekki einfalt að koma með einhlítt eða ítarlegt svar. Til að byrja með má til dæmis velta fyrir sér hvernig árið 2023 er ólíkt 2024 að þessu leyti. Spurning af þessu tagi er dæmi um stærðfræðilega spurningu sem unnt er rannsaka skipulega með aðstoð forritunar. Fyrir d-lið bendi ég á talnarunu úr rafrænum gagnabanka (OEIS: A260915).
Þriðja verkefnið sem ég kynni hér muna eflaust einhverjir þátttakendur námstefnunnar eftir, enda sátu nokkrir þeirra fram eftir við að leysa úr því. Á mynd 6 eru 32 hringir. Verkefnið gengur út á að raða öllum heiltölum frá 1-32 í hring þannig að sérhver summa aðliggjandi talna sé ferningstala. Til dæmis gæti komið til greina að setja 3 og 8 sitt hvorum megin við 1 þar sem 1+3=4 er ferningstala og 1+8=9 er ferningstala. (Í viðauka er mynd til stuðnings við úrlausn verkefnisins.)
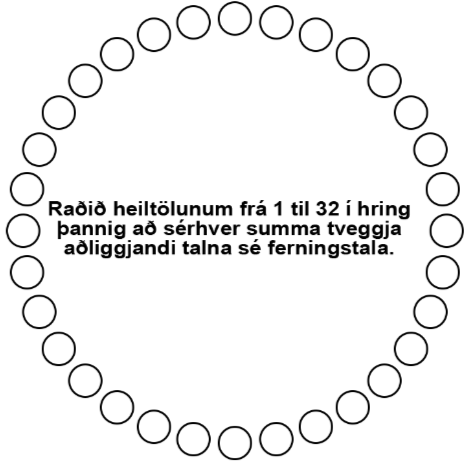
Mynd 6. Þraut sem gengur út á að raða heiltölunum 1-32
þannig að sérhver summa tveggja aðliggjandi talna sé ferningstala.
Einhverjum gæti þótt freistandi að nota ráðleggingu Pólya um að byrja á að spreyta sig á að raða í styttri hring til að átta sig betur á þrautinni, svo sem að velja n=10 þannig að raðað sé heiltölum frá 1-10 með sömu skilyrðum. Því miður gengur það ekki í þessu tilfelli. Með aðstoð netafræði og forritunar má sýna að n=32 er minnsta stærð nets sem unnt er að raða í slíkan hring (eða Hamilton-rás með tungutaki netafræðinnar). Þrautina er þó unnt að leysa án þess að kunna fyrir sér í netafræði.
Niðurlag
Í greininni hef ég sagt frá og tekið dæmi um hvernig hugræn virkjun í kennslu var metin á ólíkum stigum eftir því hvernig kennsluhættir leiddu til þess að virkja hugsun nemenda í mismiklum mæli. Þá hef ég tekið nokkur dæmi um verkefni sem eru vel til þess fallin að skapa hlutlæg tækifæri til hugrænnar virkjunar. Þó vil ég undirstrika að það eru útfærð tækifæri sem trompa hin hlutlægu – þ.e. útfærsla kennara skiptir meira máli en verkefnin. Verkefni af þeim toga sem kynnt voru hér er vissulega handhægt að útfæra þannig að reyni á að nemendur hugsi og tengi saman stærðfræðilegar hugmyndir. Annars konar verkefni, svo sem þau sem kalla má æfingaverkefni, er þó vissulega hægt að útfæra í kennslustund þannig að reyni á hugsun nemenda. Svo vel megi vera kann það þó að krefjast bæði góðs undirbúnings og sérþekkingar kennarans. Hvoru tveggja eru líklega nauðsynleg skilyrði metnaðarfullrar stærðfræðikennslu. Með þeim hugmyndum sem hér hafa verið settar fram (og lesa má nánar um í skráðum heimildum) kveiki ég vonandi innblástur einhverra kennara til að stuðla enn frekar að bæði árangri og ánægju nemenda sinna í stærðfræði.
Heimildir
Grossman, P. (2015). Protocol for language arts teaching observations (PLATO 5.0). Palo Alto, CA: Stanford University.
Jóhann Örn Sigurjónsson. (2023). Quality in Icelandic mathematics teaching: Cognitive activation in mathematics lessons in a Nordic context [Doktorsritgerð]. Háskóli Íslands. https://hdl.handle.net/20.500.11815/3843
Jóhann Örn Sigurjónsson og Berglind Gísladóttir. (2020). Vitsmunaleg áskorun í stærðfræðikennslu á unglingastigi. Tímarit um uppeldi og menntun, 29(2), 149–172. https://doi.org/10.24270/tuuom.2020.29.8
Praetorius, A.-K., Klieme, E., Herbert, B., & Pinger, P. (2018). Generic dimensions of teaching quality: The German framework of Three Basic Dimensions. ZDM, 50(3), 407–426. https://doi.org/10.1007/s11858-018-0918-4
Triplett, A. M. (2011). A closer look at the 24 game. International Journal of Applied Science and Technology, 1(5), 161–164. https://www.ijastnet.com/journals/Vol_1_No_5_September_2011/20.pdf
Weingartner, E. (2021). Cognitive Activation Potential of E&S Tasks at Commercial Vocational Schools in German Speaking Switzerland. In M. Blikstad-Balas, K. Klette, & M. Tengberg (Eds.), Ways of Analyzing Teaching Quality. Potentials and Pitfalls (pp. 204–228). Scandinavian University Press. https://doi.org/10.18261/9788215045054-2021-07

Jóhann Örn Sigurjónsson er nýdoktor í stærðfræðimenntun, kennari og tölvunarfræðingur.
Viðauki – Stuðningsefni fyrir þraut á mynd 4